Tras la muerte de Alejandro Magno en
el año
¿Qué motivos inclinaron a Tolomeo a
fundar el Museo en base
a la herencia del Liceo? Los monarcas que fundaron y mantuvieron el
Museo eran
los sucesores de una familia reinante que había mostrado desde mucho
tiempo
atrás su comprensión de la relación entre ciencia y política. Los
Ptolomeos
hubieran violado uno de sus primeros deberes si no hubiesen tomado
medidas para
la formación de ingenieros, médicos, astrónomos, matemáticos,
geógrafos, etc.
Por otra parte, el Liceo siempre había debido mucho al patronazgo
macedonio.
Recordemos unos hechos por todos conocidos: Aristóteles era oriundo de
Macedonia;
su padre había sido médico en la corte de Filipo y el propio
Aristóteles había
sido tutor de Alejandro Magno; a Estratón ya nos hemos referido. El
Liceo era,
pues, un centro de influencia macedónica en Atenas.
El Museo era, como su nombre indica,
un templo de las Musas,
y su director era un sacerdote. Pero su objeto real era el de un
instituto de
investigación que se dedicara también a la enseñanza. El Museo tenía
una nómina
de algo así como un centenar de profesores que recibían un salario del
estado.
Su biblioteca, a la cual fue incorporada con el tiempo la de
Aristóteles, tenía
aproximadamente medio millón de rollos. Poseía también un zoo, jardines
botánicos, observatorio astronómico y salas de disección.
El Museo duró unos seiscientos años,
aunque los primeros
doscientos fueron los más importantes para la ciencia. A medida que los
Ptolomeos se fueron imbuyendo progresivamente de la cultura egipcia,
favorecieron cada vez menos la ciencia, hasta el punto de que Ptolomeo
IV llegó
al extremo de perseguir lo griego en Alejandría.
El fundador de la escuela alejandrina
de ingenieros fue
Ctesibo, fl. 285-
Un examen del tratado de Filón de
Bizancio nos revela el
abanico de intereses de estos ingenieros alejandrinos y la función
sociopolítica de la ciencia en ese momento. El tratado está dividido en
las
siguientes partes: Principios y aplicaciones de la palanca;
Construcción de
puertos, artillería y balística; Neumática o máquinas que funcionan con
aire
comprimido; Construcción de autómatas; y Defensa i sitio de ciudades.
Como
puede observarse las aplicaciones bélicas absorbían la mayor parte de
la
mecánica. No tocaron el tema de la ingeniería civil ni problemas
artesanales,
si exceptuamos lo relativo a la construcción de puertos.
En el siglo III a.C. se produjo una
explosión de actividad
en el campo médico y biológico, bajo el gobierno de los primeros
ptolomeos,
dándose una segunda explosión en el siglo II d.C., bajo los romanos.
El primer maestro médico de
Alejandría fue Herófilo de
Calcedonia, fl. c. el año
Erasístrato de Quíos, fl.
300-
Erasístrato, al igual que su maestro
Estratón del Liceo, era
una especie de experimentalista. Pesó un pájaro en su jaula y observó
que
perdía peso continuamente ente comidas.
También se interesaba en los
problemas pneumáticos
estudiados por su maestro, confiriendo gran importancia a la función
del aire
en su fisiología. Estratón había mostrado de qué manera un vacío
parcial ejerce
atracción sobre los líquidos y, a la inversa, cómo los líquidos pueden
ejercer
una tracción sobre el aire. Erasístrato pensaba que por este
procedimiento el
aire era atraído hacia el cuerpo merced a la tracción de la sangre al
descender
por el cuerpo, siendo expelido cuando subía de nuevo. Normalmente,
pensaba, las
arterias están llenas de aire, o más bien de aire transformado en
espíritu
vital (pneuma), ya que había encontrado que las
arterias se hallaban
vacías en los animales muertos. Sostenía que, en los animales vivos,
cuando se
corta una arteria, el aire se escapa seguido por la sangre. Una vez que
el aire
entraba en el cuerpo, pasaba por los pulmones al corazón, donde se
transformaba
en espíritu vital. El espíritu vital era distribuido por las arterias a
todo el
cuerpo, llegando una pequeña porción al cerebro, donde se transformaba
en
espíritu animal que era distribuido por los nervios.
La escuela de Alejandría decayó en el
siglo II a.C. teniendo
la medicina que encontrar cobijo en otra parte, sobre todo en Asia
Menos
continental. Cratevas (120-
Aristarco nació en
Las principales tesis del sistema
astronómico de Aristarco
son las siguientes:
a) Las estrellas fijas y el sol
permanecen inmóviles. La
tierra y los planetas se mueven alrededor del sol, que ocupa el centro
del
universo. La tierra gira alrededor del sol en el período de un año,
pero
también gira sobre su eje diariamente. Las órbitas de la tierra y los
planetas
son circulares.
A pesar de sus indudables méritos,
Aristarco no fue el primer
astrónomo en plantear el supuesto del heliocentrismo ni el movimiento
de la tierra.
Hallamos una anticipación del heliocentrismo en el sistema de
Heráclides Ponto
(388-
Arquímedes afirma que Aristarco
planteó sus ideas
astronómicas en forma de hipótesis, lo cual tal vez quiera decir que
las
afirmaciones de heliocentrismo y movimiento de la tierra no guardan un
compromiso con la auténtica realidad (geocéntrica y geoinmovilista):
"Pero Aristarco de Samos produjo un
libro que consistía
en ciertas hipótesis cuyas premisas llevaban a la conclusión de que el
universo
es varias veces mayor de lo que ahora llamamos así. Las hipótesis son
que las
estrellas fijas y el Sol permanecen quietos, que la tierra gira
alrededor del
Sol en la circunferencia de su círculo, con lo que el Sol descansa en
el medio
de su órbita, y que la esfera de las estrellas fijas, situada sobre el
mismo
centro que el Sol, es tan grande que el círculo en el que supone que
gira la
Tierra guarda tal proporción respecto a la distancia a que se
encuentran las
estrellas fijas como la que existe entre el centro de la esfera y su
superficie". (Arenario, I)
Haría falta establecer el sentido
estricto del término
"HIPÓTESIS" en la antigüedad. P.e. del sistema de Eudoxo ya se dice,
en la historia de Eudemo, que se trata de una hipótesis, o sea, de un
supuesto
explicativo. ¿Qué grado de compromiso ontológico tiene un supuesto
explicativo?]
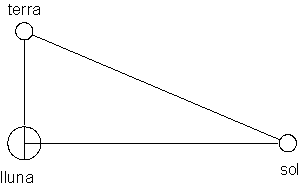
c) Dimensiones y distancia de sol,
luna y tierra: Aristarco
supuso que cuando se veía la media luna, el sol, la luna y la tierra
formaban
un triángulo rectángulo con la luna en el ángulo recto; a partir de
estas
posiciones era posible determinar las distancias relativas del sol y la
luna
midiendo la separación angular del sol y la luna respecto de la tierra.

Su medición de dicho ángulo arrojaba un
valor de 87º (el
valor real es de 89º 52&rsquo), de donde calculaba que el sol
se hallaba 19
veces más lejos de la tierra que la luna. La proporción real es de 400
veces.
Aristarco aprovechó también el
fenómeno de los eclipses de
sol y de luna para medir las dimensiones relativas de estos astros.
Dado que
por regla general la luna cubre exactamente al sol durante los eclipses
solares, Aristarco suponía que el diámetro del sol era 19 veces mayor
que el de
la luna. Los eclipses de luna proporcionaron a Aristarco la posibilidad
de
medir el diámetro de la luna respecto de la tierra. Aristarco midió la
sombra
que proyecta la tierra sobre la luna en un eclipse de luna, y lo hizo
cronometrando el tiempo que tarda la luna en pasar a través de esa
sombra. El
resultado fue que la tierra tiene un diámetro 3 veces mayor que el de
la luna.
Por consiguiente, el diámetro del sol sería entre 6 y 7 veces el de la
tierra.
Lo realmente importante de los
cálculos de Aristarco no es
el resultado (que en ocasiones se aleja mucho del valor verdadero
debido a la
deficiencia de los instrumentos de medida), sino la utilización de
métodos
geométricos y trigonométricos para la medición de las distancias
celestes.
Matematización del cosmos, transformación de sus dimensiones en un
dominio (se
abre la posibilidad de recorrerlo, se vuelve asequible, lejano pero no
infinito).
Nació en
También
se dedicó a realizar estudios geográficos. Reunió
los trabajos de sus predecesores que habían desarrollado la idea de que
la
tierra era un globo con dos polos y un ecuador, y levantó un mapa de la
tierra
conocida con líneas de latitud y longitud, separando cinco zonas, dos
frías,
dos templadas y una tórrida. Como meridiano de longitud fundamental
eligió el
de Asuán y Alejandría que, según creía, pasaba por Bizancio. Como
paralelo de
latitud fundamental tomó la línea de los 36 º que pasa por el estrecho
de
Gibraltar y la isla de Rodas. Eratóstenes pensaba que la tierra se
extendía
78.000 estadios a lo largo de este paralelo, del Atlántico al Pacífico,
siendo
el resto mar.
Apolonio de Pérgamo intentó explicar
algunos inconvenientes
del sistema astronómico eudoxiano, como p.e. la variación del brillo y
la
magnitud aparentes de ciertos planetas (Venus y Marte) y del sol, tal y
como se
observa desde la tierra. En principio tales variaciones deberían estar
justificadas por una variación de la distancia entre estos planetas y
la
tierra, pero esto planteaba un serio inconveniente: cómo hacer
compatible dicha
variación con las órbitas circulares. Apolonio diseñó dos expedientes
geométricos que, con el tiempo, tendrían un gran éxito: a) el sistema
de
epiciclos y deferentes, y b) las órbitas excéntricas.
Apolonio afirmaba que, si un planeta
se movía por un
círculo, el epiciclo, cuyo centro se movía por otro círculo, el
deferente, con
centro en la tierra, entonces la distancia del planeta había de variar,
con lo
que eligiendo adecuadamente los círculos, se podía explicar
cuantitativamente
los movimientos de los planetas.
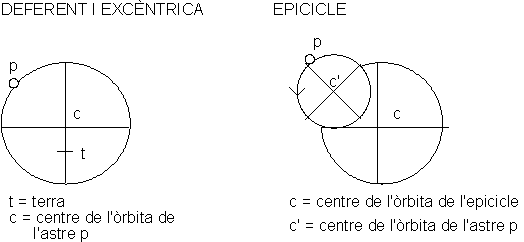
Otro expediente consistía en sugerir
que los cuerpos
celestes se movían en círculos excéntricos respecto de la tierra,
hallándose
los centros de sus órbitas a cierta distancia del centro de la tierra.
Ambos expedientes serán defendidos al
unísono por el astrónomo
Hiparco de Nicea.
Hiparco nació en
a) Resulta especialmente importante
la aportación de Hiparco
a la astronomía de observación. Hiparco, basándose en estudios
babilónicos, de
astrónomos alejandrinos y, sobre todo, en sus propias observaciones,
realizó un
catálogo de 1080 estrellas, cada una de ellas con su nombre, posición y
magnitud
(determinó seis grados de magnitud). Este catálogo no ha llegado hasta
nosotros. Se dice también que Hiparco descubrió una nueva estrella
aparecida en
su tiempo (probablemente una estrella "nova"):
"Hiparco, que nunca será alabado en
demasía (...)
descubrió una nueva estrella aparecida en su tiempo. Debido a su
movimiento el
día en que hizo su aparición, empezó a preguntarse si lo mismo
sucedería con
frecuencia y si las estrellas que se consideran fijas no podrían
también
moverse. Hizo algo que resultaría admirable incluso en un dios, contó
las
estrellas y constelaciones para las futuras generaciones y les dio a
todas
nombres. A este fin diseñó instrumentos mediante los cuales asignó luna
posición y tamaño a cada estrella y como resultado de ello es fácil
distinguir
no sólo si las estrellas están muriendo o naciendo, sino además si se
mueven de
su lugar y si su luz está aumentando o decreciendo" (Plinio, Historia
natural)
b) Otra de las grandes aportaciones
de Hiparco fue el
descubrimiento de la precesión de los equinoccios. Hiparco observó que
la
posición de las estrellas fijas respecto de los puntos equinocciales i
solsticiales había cambiado a lo largo de las observaciones de los
astrónomos
alejandrinos durante los últimos 150 años. Esto demostraba que los
solsticios y
los equinoccios variaban su posición a lo largo del tiempo.
c) Calculó también la duración del
mes lunar con un error
inferior a un segundo. Mejoró los cálculos de Aristarco sobre las
distancias
sol-luna-tierra (al observar la altitud de la luna en dos latitudes
diferentes,
descubrió que la luna se hallaba a unos 36 diámetros terrestres, lo que
resulta
un poco grande, si bien constituye una considerable mejora respecto al
valor de
9 diámetros terrestres obtenido por Aristarco a partir del ángulo
subtendido por
la luna para un observador terrestre).
El estoico Posidonio de Apamea (131-

Nació el año 85 y murió en 165. Vivió
en Alejandría y
realizó observaciones astronómicas entre los años 127 y 147. Escribió
un enorme
tratado de astronomía en 13 volúmenes que tituló Composición
matemática,
pero que es más conocido por el nombre que los traductores árabes le
dieron en
el siglo IV: Almagesto ("el más grande"). Después de
esta
obra, escribió las Hipótesis planetarias y Las
fases de las estrellas
fijas.
Se ocupó también de música (Los
armónicos) y de
geografía (Guía geográfica, obra que se imprimió
hasta el siglo XVI).
Ptolomeo, en la línea de la
astronomía alejandrina, se lanza
sobre el viejo problema platónico de "salvar las apariencias", o sea,
al diseño de un sistema geométrico que dé cuenta de los fenómenos
astronómicos.
Ptolomeo aborda este problema contando con los siguientes expedientes
tomados
de colegas que ya han trabajado antes que él, especialmente de Hiparco:
- geocentrismo
- geoestatismo
- órbitas circulares
-órbitas excéntricas
-sistema de epiciclos.
Sobre la vida de Euclides existen
pocos datos dignos de
crédito. Podemos estimar que Euclides alcanzó su madurez en torno al
año
Euclides escribió por lo menos una
decena de obras. Hoy
disponemos de dos: los Elementos (stoicheîa)
y los Datos
(Dedoména).
Los Elementos son
un conjunto de 23 definiciones, 5
postulados, 5 nociones comunes o axiomas y unas 465 proposiciones
distribuidas
en 13 libros. Entre los comentadores árabes se extendió la creencia de
que el
tratado incluía además otros dos libros, el XIV y el XV, que venían a
complementar el estudio de los sólidos regulares del libro XIII. Pero
el
supuesto libro XIV es obra seguramente de Hypsicles, un matemático
alejandrino,
quizas discípulo del propio Euclides. Y el presunto libro XV es un
producto
mucho más tardío que el anterior (siglo VI).
A pesar de su común identificación
con la geometría, el
tratado comprende diversos campos temáticos de la matemática elemental.
Entre
los temas figuran la teoría de la geometría plana (libros I-IV), la
teoría
generalizada de la proporción (V-VI), la teoría aritmética (VII-IX), la
teoría
de la inconmensurabilidad (X), la geometría del espacio (XI-XIII).
Pero, por
encima de todo, lo que más ha llamado la atención de los comentadores y
observadores es el carácter axiomático del tratado, en concreto el
conjunto de
definiciones, postulados y nociones comunes con el que se abre el libro
I.
Los Datos podría
tratarse de un texto auxiliar,
complementario del primero; tiene que ver con los libros I-VI y con la
práctica
del análisis geométrico como vía de resolución de problemas: en el
supuesto de
que ciertas partes de una figura estén dadas (por lo que se refiere a
su
magnitud, posición, etc.), muestra la manera de determinar otras partes
de la
figura en el mismo respecto.
Tenemos recensiones de otras dos. Una
es Fenómenos (phainómena);
se trata de una obra de astronomía compuesta sobre la base de la
geometría
esférica. La otra es Óptica (Optiká),
un tratado acerca de la
perspectiva y la visión directa donde se formula por vez primera el
principio
de la propagación rectilínea de la luz.
Para las demás obras de Euclides
contamos con referencias
más o menos completas.
De Sobre las divisiones de
figuras (Perì
diairéseon biblíon) hay una versión árabe. No quedan restos
de los Porismas
(Porísmata), obra en la cual, por lo que
parece, Euclides abordaba
cuestiones de matemática superior. Sobre cónicas debió
de ser una obra
en cuatro libros sobre las secciones cónicas, pero de ella sólo tenemos
noticias indirectas. Los dos libros de Sobre superficies (Tópoi
pròs
epiphaneía) estudiaban conos, cilindros, esferas y
posiblemente otras
construcciones sobre superficies de sólidos en revolución, tal vez en
la línea
desarrollada luego en Sobre conoides y esferoides de
Arquimedes. Parece
ser que Euclides escribió también unos Elementos de música (hai
katà
musikèn stoicheióseis). Finalmente debemos referirnos a un
escrito Sobre
paralogismos (Pseudária) que abundaba en
casos y ejercicios
dirigidos a formar y depurar el razonamiento del principiante en
matemáticas.
El término "elemento" (stoicheîon)
se
empleaba en la antigüedad con múltiples usos de diferentes contextos
(gramatical, cosmológico, astronómico, matemático). Su equivocidad es
manifiesta sin salir siquiera del contexto geométrico. Por un lado,
recibían el
nombre de Elementos las compilaciones que reunían
ciertos conocimientos
primordiales y básicos. Por otro lado, se llamaban "elementos" las
proposiciones que desempeñaban una función importante en la elaboración
deductiva y en la organización de ciertos resultados. Así, p.e.,
Aristóteles se
refiere a los términos como elementos de un silogismo.
Debemos, sin embargo, distinguir
entre un sentido amplio y
un sentido estricto de "elemento". Supongamos un desarrollo deductivo
de la forma siguiente:
A1, A2... P1, P2... Q
En la medida en que P1, P2...
funcionan como proposiciones o
pasos deductivos que llevan a la obtención de Q, cumplen la función de
elementos en sentido amplio o genérico: son elementos porque
contribuyen o
forman parte del proceso que conduce a una conclusión. Ahora bien, P1,
P2...
han sido a su vez deducidos (o sea, son conclusión de) a partir de
otros
principios que, por su parte, no han sido deducidos de otros.
Atendiendo a este
segundo sentido, se denominan "elementos" las proposiciones que
tienen el estatuto de principios (archaí) dentro de
una disciplina y
constituyen el punto de partida absoluto de un desarrollo deductivo de
otras
proposiciones que forman parte de un cuerpo sistemático de conocimiento.
De lo dicho anteriormente podemos
concluir que los Elementos
venían a ser tratados que exponían los "elementos" (en sentido
general o estricto) de algún dominio de las matemáticas. Como veremos a
continuación, Euclides no fue el primer autor de un tratado de Elementos,
pero, por lo que hoy sabemos, el de Euclides sí es el primer tratado
que: i)
distingue expresamente un conjunto determinado de "elementos"
entendidos en su sentido estricto, es decir, como primeros principios
de una
construcción deductiva aplicada a la
geometría; ii)
subdivide dichos principios en definiciones (hóroi),
postulados (aitémata)
y nociones comunes (koinaì énnoiai).
Los Elementos de
Euclides coronan una tradición de
tratados elementales hoy desaparecidos. Hipócrates de Quíos, hacia el
470-
...A B P Q
El procedimiento de Hipócrates
difiere, sin embargo, del que
utiliza Euclides en sus Elementos. Ciertamente la
proposición inicial y
las que le sirven de prueba son elementos, pero en ningún caso
principios.
Hipócrates realiza la deducción a partir de unos elementos, pero no
crea un
sistema deductivo completo (un sistema axiomático). Hipócrates
selecciona las
proposiciones iniciales no en calidad de principios geométricos
simples, sino
en función de las condiciones y supuestos oportunos para el problema
particular
que debe resolver. Este procedimiento resulta afín al señalado por
Platón en Menón,
cuando se refiere al proceder "a partir de hipótesis" que siguen los
geómetras: aquí una hipótesis viene a representar un medio de prueba en
el
sentido de constituir un supuesto a una condición a las que se
retrotrae la
solubilidad de la cuestión considerada.
Con posterioridad a Hipócrates, un
tal León, algo mayor que
Eudoxo y más joven que Platón, compuso otro tratado en la misma línea
que el de
su antecesor.
El último tratado conocido anterior
al de Euclides es el de
Teudio de Magnesia. Fue éste seguramente un manual que circuló dentro
de la
Academia platónica. Desconocemos su contenido pero es posible
conjeturar, por
ciertas referencias de Platón y Aristóteles, que los Elementos
de Teudio
contribuyeron a mejorar el orden deductivo de la geometría mediante la
institución de proposiciones geométricas primeras y simples1.
El libro I de los Elementos
contiene una cantidad
considerable de proposiciones ordenadas, basadas unas en otras, de tal
forma
que se expone en primer lugar lo que habrá de utilizarse más adelante.
Ese
conjunto de proposiciones (que en general han recibido el nombre de
"principios") se divide en: definiciones, postulados y nociones
comunes.
El libro I empieza con una serie de
23 definiciones (hóroi).
Esas definiciones son las siguientes:
1. Un punto (semeîon)
es lo que no tiene partes.2
2. Una línea es una longitud sin
anchura.
3. Los extremos de una línea son
puntos.
4. Una línea recta es aquella que
yace por igual respecto de
los puntos que están en ella.3
5. Una superficie (epipháneia)
es lo que sólo tiene
longitud y anchura.4
6. Los extremos de una superficie son
líneas.
7. Una superficie plana (epípedon)
es aquella que
yace por igual respecto de las líneas que están en ella.
8. Un ángulo plano es la inclinación
mutua de dos líneas que
se encuentran una a otra en un plano y no están en línea recta.
9. Cuando las líneas que comprenden
el ángulo son rectas el
ángulo se llama rectilíneo.
10. Cuando una recta levantada sobre
otra recta forma
ángulos adyacentes entre sí, cada uno de los ángulos iguales es recto y
la
recta levantada se llama perpendicular a aquella sobre la que está.
11. Ángulo obtuso es el (ángulo)
mayor que un recto.
12. Ángulo agudo es el (ángulo) menor
que un recto.
13. Un límite es aquello que es
extremo de algo.
14. Una figura es lo contenido por
uno o varios límites.
15. Un círculo es una figura plana
comprendida por una línea
tal que todas las rectas que caen sobre ella desde un punto de los que
están
dentro de la figura son iguales entre sí.5
16. Y el punto se llama centro del
círculo.
17. Un diámetro del círculo es una
recta cualquiera trazada
a través del centro y limitada en ambos sentidos por la circunferencia
del
círculo, recta que también divide el círculo en dos partes iguales.
18. Un semicírculo es la figura
comprendida entre el
diámetro y la circunferencia por él cortada. Y el centro del
semicírculo es el
mismo que el del círculo.
19. Figuras rectilíneas son las
comprendidas por rectas,
triláteras las comprendidas por tres, cuadriláteras las comprendidas
por
cuatro, multiláteras las comprendidas por más de cuatro rectas.
20. De entre las figuras triláteras,
triángulo equilátero es
la que tiene los tres lados iguales, isósceles la que tiene sólo dos
lados iguales,
y escaleno la que tiene los tres lados desiguales.
21. Además, de entre las figuras
triláteras, triángulo
rectángulo es la que tiene un ángulo recto, obtusángulo la que tiene un
ángulo
obtuso, acutángulo la que tiene los tres ángulos agudos.
22. De entre las figuras
cuadriláteras, cuadrado es la que
es equilátera y rectangular, rectángulo la que es rectangular pero no
equilátera, rombo la que es equilátera pero no rectangular, romboide la
que
tiene los ángulos y lados opuestos iguales entre sí, pero no es
equilátera ni
rectangular; y llámanse trapecios las demás figuras cuadriláteras.
23. Son rectas paralelas las que
estando en el mismo plano y
siendo prolongadas indefinidamente en ambos sentidos, no se encuentran
una a
otra en ninguno de ellos.6
Una gran parte de los historiadores
han acentuado el papel
relevante de Aristóteles en el origen de la sistematización matemática
y han
tratado de aproximar la clasificación de los principios a la
aristotélica.
Aristóteles incluye la definición en
el conjunto de los
primeros principios. Una definición, piensa Aristóteles, es un puro
hecho de
significado, no existencial (la definición de "círculo", p.e., nos dice
qué es un círculo, no que sea, que exista), aunque admite que, en
geometría, es
preciso asumir la existencia de unas cuantas cosas primarias, que son
definidas, y que son la existencia de puntos y líneas. El resto de
figuras
precisa ser probado, demostrado, construido. En Aristóteles, pues, la
definición no dice nada sobre la existencia o no de la cosa definida,
que ha de
ser probada o, en algún caso, asumida.
De acuerdo con esto, también las
definiciones de Euclides
son puros hechos de significado. La Def. 4 trata de la línea recta,
pero no
afirma que puedan darse líneas rectas. Que la línea recta sea no sólo
un
significado sino algo existente pasa por construir efectivamente una
recta. Y
ello ya no puede ser una definición sino otra cosa: un postulado, en
concreto
el Post. 1; y los mismo sucede con el círculo (Post. 3). El resto de
las
definiciones son también confirmadas como existentes, no a través de
postulados
sino mediante proposiciones (así, p.e., en Elementos
I, 1 se propone
construir un triángulo equilátero (Def. 20) que, una vez acabado, se
demuestra
conforme con la definición). En todos los casos hay, pues, un paso de
las cosas
definidas, pero de las cuales no se asume la existencia, a la prueba de
su
existencia a través de la construcción (bien por postulados, bien a
través de
proposiciones).
A continuación de las definiciones,
Euclides expone una
serie de 5 postulados (aitémata):
1. Postúlese el trazar una línea
recta desde un punto
cualquiera hasta un punto cualquiera.
2. Y el prolongar continuamente una
recta finita en línea
recta.
3. Y el describir un círculo con
cualquier centro y
distancia.
4. Y el ser todos los ángulos rectos
iguales entre sí.
5. Y que si una recta al incidir
sobre dos rectas hace los
ángulos internos del mismo lado menores que dos rectos, las dos rectas
prolongadas indefinidamente se encontrarán en el lado que están los
(ángulos)
menores que dos rectos.
Aristóteles usa el término
"postulado" para
referirse a algo que se asume sin prueba aunque haya de ser demostrado.
Euclides
entiende "postulado" como una serie de cosas que es necesario asumir
sin evidencia propia: ciertas simples construcciones (el hecho de
dibujar una
línea, alargarla, dibujar un círculo) que son imprescindibles para la
construcción de otras figuras (como demuestra la Prop. 1, no se puede
construir
un triángulo equilátero sin construir líneas rectas y círculos). Dicho
de otro
modo: los postulados garantizan la existencia de ciertas formas
geométricas
básicas que aseguran la posibilidad de construir formas más complejas.
A continuación, se exponen 8 nociones
comunes (koinai
énnoiai):
1. Las cosas iguales a una misma cosa
son también iguales
entre sí.
2. Y si se añaden cosas iguales a
cosas iguales, los totales
son iguales.
3. Y si de cosas iguales se quitan
cosas iguales, los restos
son iguales.
4. Y las cosas que coinciden entre sí
son iguales entre sí.
5. Y el todo es mayor que la parte.
Las nociones comunes de Euclides se
identifican con los
axiomas aristotélicos e incluso recogen algunos ejemplos de Aristóteles
(Noc.
3). Se trata de principios que son verdaderos sin necesidad de
demostración y
que, además, tienen una validez más allá de la geometría.
Las definiciones, postulados y
nociones comunes presentadas
en el capítulo anterior son utilizadas por Euclides para la
demostración de una
serie de proposiciones (problemas y teoremas). Euclides utiliza una
especie de
pauta de prueba de las proposiciones que, cuando la sigue de forma
cabal,
comprende los siguientes pasos:
1) Enunciado (prótasis):
proposición del objeto a
construir si se trata de un problema, o del aserto a establecer si se
trata de
un teorema; su formulación perfecta declara por una parte lo que está o
se
considera dado y, por otra parte, lo que se busca probar.
2) Exposición (ékthesis):
presentación de lo dado o
introducción de un caso determinado de aplicación del enunciado
mediante la
cláusula "sea..." y el uso de letras como abreviaturas que designan
los elementos del caso (puntos, líneas, figuras, magnitudes, números).
3) Preparación (kataskeué):
urdimbre o disposición de
construcciones y relaciones, a partir de lo dado y en orden a la
obtención del
resultado propuesto.
4) Demostración (apódeixis):
proceso demostrativo
propiamente dicho que consiste en la derivación de consecuencias sobre
la base
de los conocimientos previos, ya sean proposiciones primordiales
(definiciones,
postulados, nociones comunes), ya sean proposiciones sentadas en
pruebas
anteriores.
5) Conclusión (sympérasma):
confirmación de que el
objeto de prueba ha sido establecido.
Vamos a ver algunos ejemplos
extraídos del libro I de Elementos
que ilustran el funcionamiento de este método de demostración
matemática:
PROPOSICIÓN 1
ENUNCIADO (proposición del
objeto a construir, pues se
trata de un problema)
"Construir un triángulo equilátero
sobre una recta
finita dada".
EXPOSICIÓN:
"Sea AB la recta finita dada. Así
pues, hay que
construir sobre la recta AB un triángulo equilátero".
PREPARACIÓN:
"Descríbase con el centro A y la
distancia AB el
círculo BCD (Post. 3), y con el centro B y la distancia BA descríbase a
su vez
el círculo ACE (Post 3), y a partir del punto C donde los círculos se
cortan
entre sí, trácense las rectas CA, CB hasta los puntos A, B (Post. 1)".
DEMOSTRACIÓN:
"Y puesto que el punto A es el centro
del círculo BCD,
AC es igual que AB (Def. 15); puesto que el punto B es a su vez el
centro del
círculo ACE, BC es igual que BA (Def. 15); por tanto, cada una de las
rectas
CA, CB es igual que AB. Ahora bien, las cosas iguales a una misma cosa
son
también iguales entre sí (N.C. 1); por tanto, CA es también igual que
CB; luego
las tres CA, AB, BC son iguales entre sí".
CONCLUSIÓN:
"Por consiguiente, el triángulo ABC
es equilátero y ha
sido construido sobre la recta finita AB. Que es lo que había que
hacer".
Como puede verse, esta proposición
plantea construir una
determinada figura geométrica -un triángulo equilátero- de la que ya se
ha
proporcionado la definición (Def. 20) pero que todavía no se ha
demostrado que
pueda efectivamente darse.
La demostración de que el triángulo
equilátero es algo
"real" (o sea, construible, diseñable) se lleva a cabo mediante el
recurso a los principios básicos expuestos al comienzo del libro 1, es
decir,
postulados, nociones comunes y definiciones. En concreto, en esta
proposición,
Euclides utiliza el Post. 1 ("Trazar una línea recta entre dos
puntos"); el Post. 3 ("Trazar un círculo") en dos ocasiones; la
Def. 15 ("Todos los radios de una circunferencia son iguales entre
sí") en dos ocasiones; y la N.C. 1 ("Las cosas iguales a una misma
cosa son iguales entre sí"). Con estos recursos, previamente definidos,
Euclides construye el triángulo equilátero.
A continuación ofrecemos el
desarrollo de la proposición 2
que, como veremos, no sólo utiliza los principios básicos sino también
la
construcción demostrada en la proposición 1.
PROPOSICIÓN 2
"Poner en un punto dado (como
extremo) una recta igual
a una recta dada.
Sea A el punto dado y BC la recta
dada.
Así pues, hay que poner en el punto A
una recta igual a la
recta dada BC.
Trácese, pues, desde el punto A hasta
el punto B la recta AB
(Post. 1) y constrúyase sobre ella el triángulo equilátero DAB (Prop.
I, 1), y
sean AE, BZ el resultado de prolongar en línea recta las rectas DA, DB
(Post.
2); y con el centro B y la distancia BC descríbase el círculo CHP
(Post. 3), y
a su vez con el centro D y la distancia AH, descríbase el círculo HLK
(Post.
3).
Así pues, como el punto B es el
centro del círculo CHP, BC
es igual a BH. Como a su vez el punto D es el centro del círculo HLK,
DL es
igual a DH, cuyas partes respectivas DA y DB son iguales. Luego la
parte
restante AL es igual a la parte restante BH (N.C. 3). Pero se ha
demostrado que
también BC es igual a BH; por tanto, cada una de las rectas AL, BC es
igual a
BH. Y las cosas iguales a una misma cosa son también iguales ente sí
(N.C.1);
luego AL es también igual a BC.
Por consiguiente, en el punto dado A se ha puesto la recta AL igual a la recta dada BC. Q.E.F."
Arquímedes de Siracusa matemático, físico e inventor griego, nace en Siracusa (¿285-212 a.J.C). Su padre, Fidias, posiblemente astrónomo, parece que influyó en su vocación y formación. Estudió en la famosa escuela de Alejandría, posiblemente fuera alumno de Euclides, y regresó a su ciudad natal donde dedicó su vida a la investigación.
Las aportaciones de Arquímedes a las matemáticas fueron de gran categoría científica. Su método fue fundamentalmente geométrico, obteniendo conclusiones que no sólo representaron un gran avance sobre la geometría, sino que también llevan al cálculo integral. Fue el primer matemático conocido del que se tienen nocicias que calculó el área limitada por un segmento parabólico en el intervalo [0,1], determinando la suma de las áreas de los rectángulos incritos y circunscritos.
En Geometría sus escritos más importantes fueron:
* De la Esfera y el Cilindro, donde introduce el concepto de
concavidad, que Euclides no había utilizado, asi como ciertos
postulados referentes a la linea recta.
* De los Conoides y Esferoides en donde define las figuras engendradas por la rotación de distintas secciones planas de un cono.
* De las Espirales en donde analiza estas importantes curvas y analiza sus elementos más representativos.
En Aritmética son, fundamentalmente dos los escritos más interesantes:
* El Arenario en el que expone un método para escribir números muy
largos dando a cada cifra un orden diferente según su posición.
* De la medida del Círculo una de sus obras fundamentales, donde demuestra que la razón entre la circunferencia y el diámetro está comprendida entra 3 10/7 y 3 1/7; dicha relación es conocida en la actualidad por . Demuestra además la equivalencia entre el área del círculo y un triángulo rectángulo cuyos catetos son el radio y el perímetro (longitud) de la circunferencia.
Arquímedes
comunicó a Eratóstenes (bibliotecario de Alejandría) los razonamientos
seguidos en las custiones geométricas. Los mismos se recogen en una
obra fundamental: El Método. (Algo así, según algunas investigaciones,
como una comunicación entre colegas al más alto nivel).
Las aportaciones más importantes de Arquímedes a la Física se centran en la mecánica de sólidos y en la Hidrostática, en las que se vale para sus demostraciones de figuras geométricas. En la mecánica de sólidos es la Estática la parte que má mereció su atención. En sus escritos trata sobre el equilibrio de los cuerpos geométricos, así como la forma de determinar el centro de gravedad de cualquier cuerpo (en estos escrito habla del centro de gravedad de las figuras planas)
También
enuncia la ley fundamental de la palanca, la cual produjo gran
sensación en el mundo griego (Dadme un punto de apoyo y moveré el
mundo). La polea compuesta, basada en el principio de la palanca, y que
empleó para mover un gran barco, para sorpresa del escéptico rey
Hierón, fue otrode sus sorprendentes descubrimientos. El historiador
Plutarco nos cuenta "[...] que no podía ser deslizado del muelle a no
ser que se emplease un gran esfuerzo y muchos hombres; y, tras cargarlo
con numeroso pasaje y mercancías a tope, se sentó a una cierta
distancia y, sin gran esfuerzo, sino sólo sosteniendo el cabezal de la
polea en su mano y tirando de las cuerdas gradualmente, arrastró el
barco en línea recta, de forma suave y por igual como si se estuviera
moviendo en el mar"
Probablemente el descubrimiento más conocido
de Arquímedes sea la ley sobre la pérdida que sufren los cuerpos
sumergidos en un líquido. Arquímedes descubrió con dicho principio que
el rey Hierón había sido objeto de una estafa al encargar una corona de
oro. Cuenta la tradición que descubrió la solución mientras se estaba
bañando y salió corriendo desnudo de su casa gritando (¡lo he
descubierto!).
Arquímedes aplicó parte de sus descubrimientos en la defensa de su ciudad natal contra el asedio de los romanos. Citando nuevamente a Plutarco, las legiones romanas avanzaron hacia las murallas creyéndose invencibles "[...] pero cuando Arquímedes comenzó a maniobrar con sus máquinas, inmediatamente lanzó contra las fuerzas terrestres toda clase de armas arrojadizas y unas masas inmensas de piedras que caían con un ruido y violencia terribles; contra las cuales ninguno pudo resistir, ya que abatían a cuantos les caían a montones, rompiendo toda formación."
Cuenta la tradición, aunque no parece muy probable, que mediante unos espejos incendió la flota romana desde el interior de las murallas de Siracusa; parece ser que el artilugio consistía en un conjunto de espejos planos con los que concentraba los rayos del sol sobre las velas de las embarcaciones.
Muerte de Arquímedes
Pero
a pesar de todas sus invenciones y grandes armas, la verdadera pasión
de Arquímedes fueron las matemáticas puras "[...] sus palancas, poleas
y catapultas fueron naderías en comparación con los bellos teoremas que
descubrió". Nuevamente citamos a Plutarco: "Arquímedes poseía un
espíritu tan elevado, un alma tan profunda y con tales tesoros de
conocimientos científicos que, aunque estos inventos le han traído
hasta ahora el renombre de una gran sagacidad sobrehumana, no se ha
dignado dejarnos ningún comentario o escrito sobre estas materias; sino
que repudiando como sórdido e innoble el mundo de la ingeniería y toda
clase de técnica que sólo sirve para mero uso y provecho, situó sus
afectos y ambiciones en aquellas especulaciones más puras en las que no
puede caber ninguna referencia a las vulgares necesidades de la vida"
Su máximo legado fueron las matemáticas y, en ese terreno, permanece como el más grande de la antigüedad. Sus resultados, que sobreviven en una docena de libros y fragmentos, tienen una calidad y un refinamiento lógico verdaderamente sorprendentes.
Cuando Siracusa fue
capturada por los soldados de Marcelo un destacamento entró en la casa
de Arquímedes que se encontraba absorto en sus trabajos y le dio muerte.
Plutarco nos relata, por último, el epitafio que pidió a sus amigos que figurara sobre su tumba:
"[...] sus descubrimientos fueron numerosos y admirables; pero se cuenta que le pidió a sus amigos y parientes que, cuando muriera, colocaran sobre su tumba una esfera dentro de un cilindro, incribiéndola en la proporción del sólido continente respecto al contenido, esto es, la razón 3:2"
______________________________________________________________________________________________
1 Platón, en la República,
da
a entender que el método de las hipótesis de los geómetras ya no sólo
consiste
en el análisis de problemas, sino que ha iniciado una conversión
sintética
hacia la deducción de teoremas: la geometría ha empezado a instituir
ciertas
proposiciones como principios de los que ya no cabe dar razón, pues los
geómetras los toman como si fueran obvios para cualquiera y, partiendo
de
ellos, deducen el resto hasta concluir en el objeto final de la prueba.
Aristóteles da muestra también del cambio metodológico pues declara que
son
elementos "las proposiciones geométricas cuyas demostraciones están
contenidas en las pruebas de otras proposiciones, de todas o de la
mayoría" (Metafísica B 3, 998a25-26) y que "las
demostraciones
primeras e implícitas en otras demostraciones se llaman elementos" (Metafísica
D 3, 1014a35-b2).
2 La definición recoge la idea tradicional de punto como aquello que es indivisible en partes. Pero no incurre en el error (que Aristóteles atribuye ya a las definiciones habituales de su tiempo) de definir lo anterior por referencia a lo posterior: el punto como límite a la línea, la línea como límite de la superficie, la superficie como límite del cuerpo sólido.
 Lic.CC.2.5  |